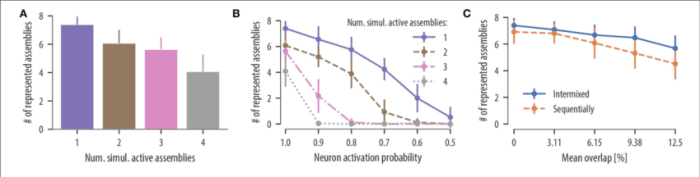
Two parallel lines cut by a transversal worksheet answers – The study of parallel lines cut by a transversal is a fundamental concept in geometry with wide-ranging applications in various fields. This worksheet provides comprehensive answers to common questions, offering a thorough understanding of the properties, relationships, and theorems associated with this topic.
Delve into the world of parallel lines and transversals, exploring their practical applications and solving problems with ease.
This worksheet delves into the intricacies of parallel lines and transversals, examining their properties, relationships, and theorems. Through clear explanations, engaging examples, and thought-provoking problems, it empowers learners to grasp the fundamental concepts of geometry.
1. Line Properties and Relationships
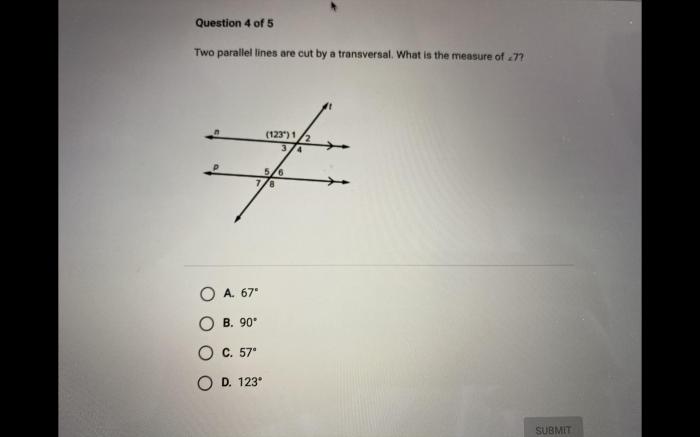
Parallel lines are two lines that never intersect. They maintain a constant distance from each other, no matter how far they are extended. Some important properties of parallel lines include:
- If two lines are parallel to a third line, then they are parallel to each other.
- If two lines are perpendicular to the same line, then they are parallel to each other.
- If two lines have the same slope, then they are parallel to each other.
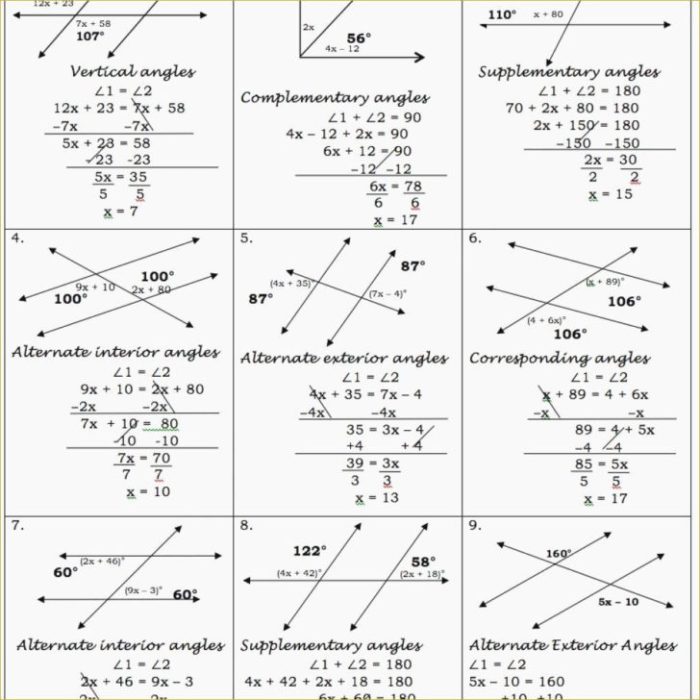
When a transversal intersects two parallel lines, it creates eight angles. These angles can be classified into four types:
- Corresponding angles are angles that are in the same position relative to the transversal.
- Alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines.
- Alternate exterior angles are angles that are on opposite sides of the transversal and outside the parallel lines.
- Same-side interior angles are angles that are on the same side of the transversal and inside the parallel lines.
2. Angle Relationships
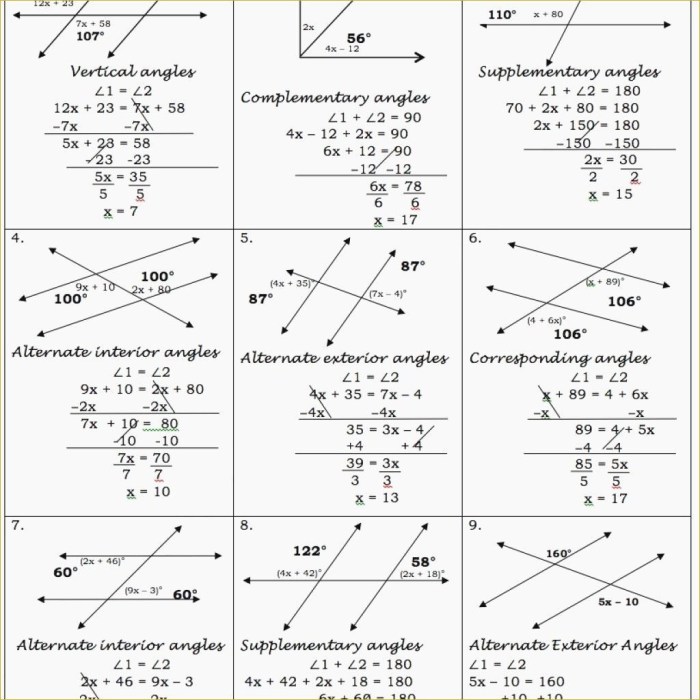
When two parallel lines are cut by a transversal, the following angle relationships hold true:
- Corresponding angles are congruent.
- Alternate interior angles are congruent.
- Alternate exterior angles are congruent.
- Same-side interior angles are supplementary (add up to 180 degrees).
These angle relationships can be used to solve problems involving parallel lines and transversals. For example, if you know the measure of one corresponding angle, you can find the measure of the other corresponding angle.
3. Proofs and Theorems
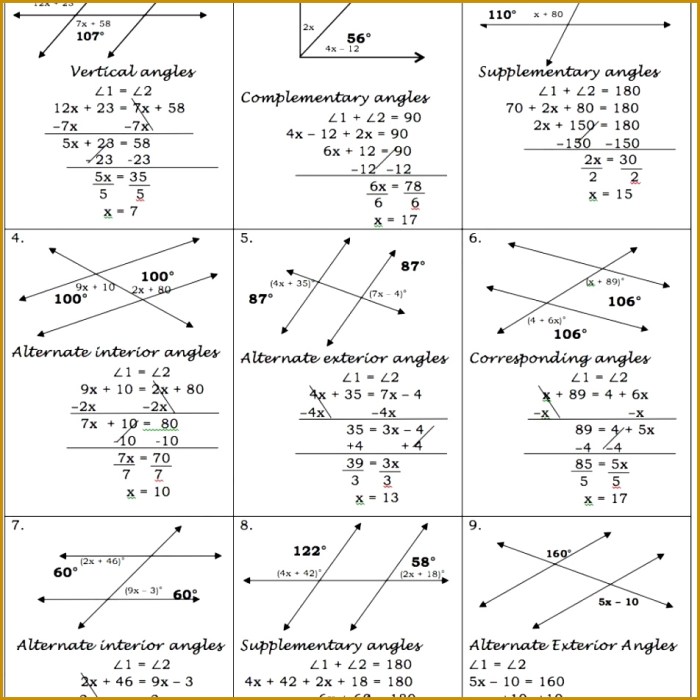
There are several theorems related to the angle relationships of parallel lines cut by a transversal. These theorems include:
- The Converse of the Corresponding Angles Theorem: If two lines are cut by a transversal and the corresponding angles are congruent, then the lines are parallel.
- The Converse of the Alternate Interior Angles Theorem: If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
- The Converse of the Alternate Exterior Angles Theorem: If two lines are cut by a transversal and the alternate exterior angles are congruent, then the lines are parallel.
- The Same-Side Interior Angles Theorem: If two lines are cut by a transversal and the same-side interior angles are supplementary, then the lines are parallel.
These theorems can be proven using geometric reasoning and algebraic principles.
4. Applications and Examples
The theorems and relationships related to parallel lines cut by a transversal have many applications in real-world situations. For example, they are used in:
- Architecture: to design buildings that are structurally sound
- Engineering: to design bridges and other structures that can withstand stress
- Surveying: to measure distances and angles
- Navigation: to determine the location of a ship or airplane
Below is a worksheet with problems that demonstrate the applications of these concepts.
Question & Answer Hub: Two Parallel Lines Cut By A Transversal Worksheet Answers
What is the definition of parallel lines?
Parallel lines are two lines that never intersect, no matter how far they are extended.
What is a transversal?
A transversal is a line that intersects two or more other lines at distinct points.
What are corresponding angles?
Corresponding angles are pairs of angles that are located in the same position relative to the transversal and the parallel lines.
What is the Alternate Interior Angles Theorem?
The Alternate Interior Angles Theorem states that if two parallel lines are cut by a transversal, then the alternate interior angles are congruent.